摘要：本文以二值噪声图像去噪问题为研究对象，应用概率图模型理论，建立去噪问题的马尔科夫随机场模型，将去噪问题转化为优化问题，并应用ICM算法进行优化求解。编制了Python程序，并进行数值仿真实验，结果表明，去噪效果令人满意。

数学准备

在机器学习领域，概率图模型(Graphical Model)是一种将问题抽象成数学模型的高效建模方法，具有很强的表达能力。借助于概率图模型，很多机器学习的方法都可以用概率图模型来表示。

概率图模型是综合了图论和概率论的知识。根据图的不同，概率图模型可以分为三类：

- 1）有向图(directed graph)，也称贝叶斯网(Bayesian Network) 
- 2）无向图(undirected graph)，也称马尔科夫随机场(Markov Random Filed)
- 3）因子图(Factor graph)

三类图模型有各自优缺点，适应于不同的对象。本文的采用马尔科夫随机场模型。

图模型

马尔科夫随机场定义在无向图上，因此我们先介绍无向图的定义：一个无向图表示为$G=(V,E)$，其中$V$是图的顶点集(Vertex set)，$E$代表(无向)边集合(Edge set)。一个典型的无向图如下图所示：

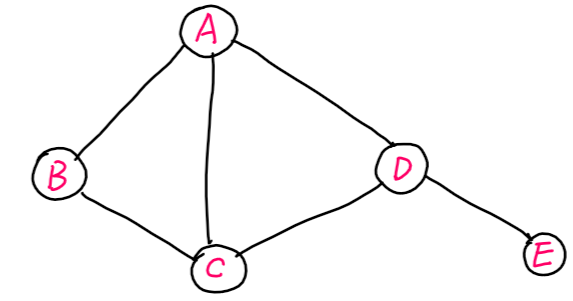
其中:顶点集$V=\left\{ A,B,C,D,E\right\}$,边集合$E=\{(A,B),(B,C),(A,C),(A,D),(D,E)\}$，注意到边集合中的的元素是两个顶点的无序对的形式，即交换前后位置不改变边，如$(A,B)$和$(B,A)$代表同一条边。

最大团

给定一张图$G=(V,E)$，和顶点集合的一个非空子集合$C\subset V$，如果$C$中任何两个顶点之间均有边链接，则称$C$为团(clique)；更进一步，若加入任何一个顶点$v \in G \backslash C$中的顶点，都使得$ C \cup {v}$不再是团,则称$C$为最大团(maximal clique)。

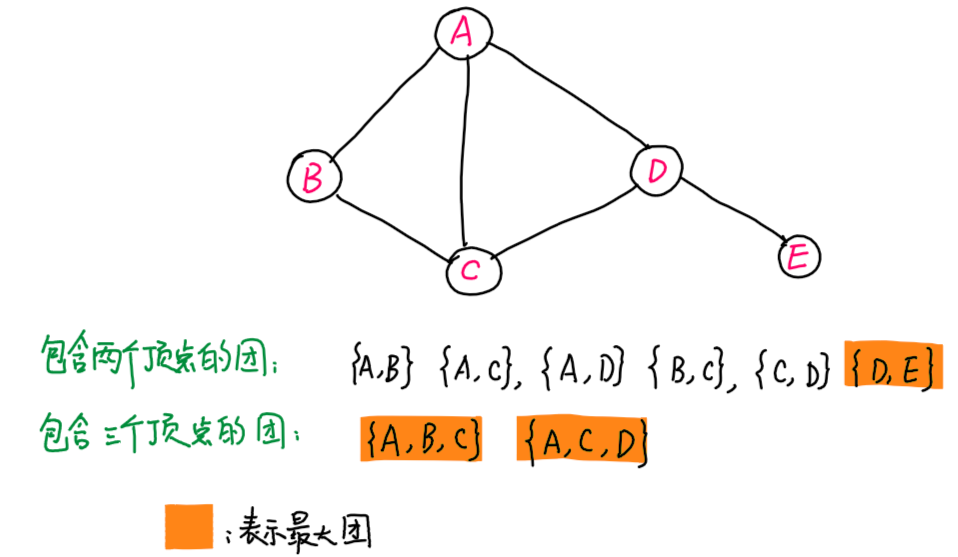
上述定义比较抽象，可用下图辅助理解：

对于团，任何两点之间都有边链接。例如，由一条边连接的两个顶点，自然成为一个团，如$\{A,B\}$，$\{A,C\}$等.
对于最大团，如果再增加任何一个顶点，就不再成为团。
— 对于团$\{A,B\}$,还可以增加顶点$C$,形成团$\{A,B,C\}$,该团中任何两点都有边连接。因此，$\{A,B\}$不是最大团
— 对于团$\{D,E\}$,我们看到，增加任何一个顶点，无法保证两点之间有边存在，例如，增加点$C$，则$\{C,D,E\}$中，不存在边$(C,E)$，因此$\{D,E\}$是最大团。

马尔科夫随机场

在无向图的基础上，我们用顶点代表一个随机变量(Random variable)，用边代表随机变量之间的依赖关系，这样，无向图就代表了众多变量之间的”联合”。而马尔科夫随机场就是一种特殊的无向图，其特殊性在于，变量的联合密度函数(joint probability density function，jpdf)可以根据图直接写出来：

$P(X)=\frac{1}{Z}\prod_{C}\phi_C (X_C) \tag{1}$

其中$C$是图$G$上的最大团。$Y_C$表示$C$对应的随机变量。需要注意的是，连乘$\prod_{C}$中，$C$要取遍所有的最大团。$\phi_C$是C上的势函数(potential function),要求严格为正。

$Z=\sum_{X}\prod_{C} \phi_C(X_C)$

称为规范化因子(Normailization Factor)，用于保证公式(1)概率密度函数是良定的(well defined)，即$\sum_X P(X)=1 $.

对于下图：

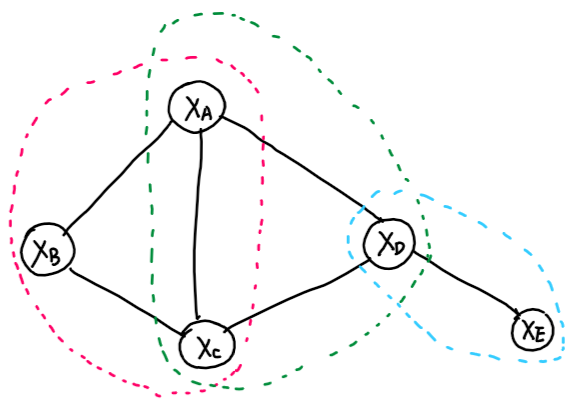
我们可以写出其联合概率密度函数：

$\begin{aligned} & P(X_A,X_B,X_C,X_D,X_E)\\ =& \frac{1}{Z} \color{red}{\phi_1 (X_A,X_B,X_C)} \color{green}{\phi_2 (X_A,X_C,X_D)}\color{blue}{\phi_3 (X_D,X_E)} \end{aligned}$

其中

$Z=\sum_{\small X_A,X_B,X_C\\ \small X_D,X_E} \color{red}{\phi_1 (X_A,X_B,X_C)} \color{green}{\phi_2 (X_A,X_C,X_D)}\color{blue}{\phi_3 (X_D,X_E)}$

注意到，势函数$\phi_i,i=1,2,3$分别对应三个最大团。

问题描述

有了上述数学准备，就可以对图像去噪问题进行数学建模。我们知道，一张数字图像在电脑中是以矩阵的形式存储的。例如，一张黑白照片可以是是一个行数1280，列数720的矩阵，矩阵中每一个元素代表一个像素.假设下图：

是一张真实图片(ground truth)。
假设因为某些原因，例如图像传输过程中受到干扰，我们得到如下所示的噪声图片(noise image):

现在的问题是：如何通过某些方法恢复出真实图像的样貌。

借助于马尔科夫随机场理论，可以对此问题进行数学建模：将图像中的素点看做随机变量，则整副图像就是随机变量的集合，对于噪声图像和真实图像分别有：

$X =\{ X_{mn} | m=1,\cdots,M; n=1,\cdots,N\} \\ Y =\{ Y_{mn} | m=1,\cdots,M; n=1,\cdots,N\}$

其中，$M$和$N$是图像的尺寸。噪声图像包含的变量$X$是已观测变量，真实图像包含的变量$Y$是未观测变量。

我们有了一张噪声图片，相当于对随机变量集合$X$进行了一次采样,得到了$X$的采样值$\mathbf{x}$,现在我们想知道$Y$的后验概率是多少，即:

$P(Y|X=\mathbf{x})$

并希望找到$\mathbf{y}$使得$P(Y=\mathbf{y}|X=\mathbf{x})$最大.即如下的最优化问题：

$\arg\max_Y P(Y|X=\mathbf{x}) \tag{2}$

上式是条件概率。根据全概率公式：

$\begin{aligned} P(Y|X=\mathbf{x})&=\frac{P(Y,X=\mathbf{x})}{P(X=\mathbf{x})}\\ & \\ \color{red}{\text{正比于}\rightarrow}& \propto P(Y,X=\mathbf{x}) \end{aligned}$

由于$P(X=\mathbf{x})$是常数，我们不关心。因此(2)中的最优化问题可以转化为求$P(Y,X=\mathbf{x})$的最大化问题，即：

$\arg\max_Y P(Y|X=\mathbf{x})\quad \stackrel{等价于}{\Longleftrightarrow}\quad \arg\max_Y P(Y,X=\mathbf{x})$

现在，问题由求条件概率密度的最大值问题转变为求联合概率密度的最大值问题，我们需要知道联合概率密度的形式，而这就需要引入马尔科夫随机场，由前面的数学准备可知，如果我们得到图结构，就可以写出这个联合概率密度函数。

应用马尔科夫随机场理论建模及优化

现在，我们需要刻画这个图结构：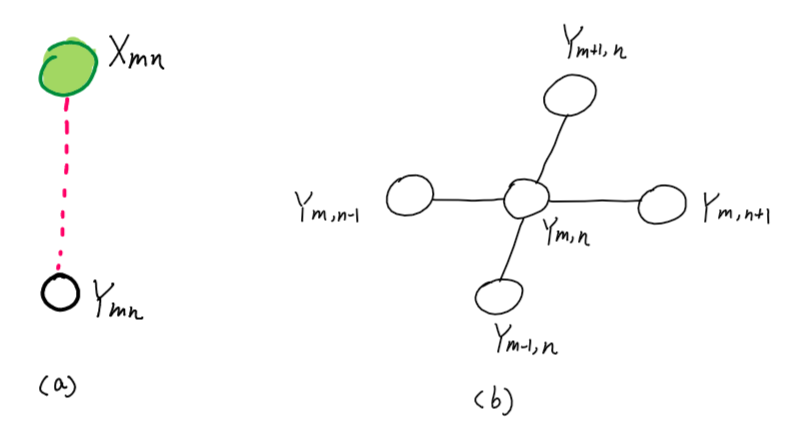
各变量之间的关系

噪声图片中的像素点认为是观测变量$X_{m,n}$，真实图片中的像素点$Y_{m,n}$为未观测变量，我们希望在真实图片和噪声图片之间建立关系，主要考虑两方面：

(a)：观测变量和未观测变量： $X_{m,n}$只与$Y_{m,n}$有关，对于上图中的(a)。
(b)：未观测变量之间：未观测点$Y_{mn}$仅与其邻居变量集合有关。邻居变量集合包含该像素点上下左右四个像素点，即$Nb(Y_{m,n})=\{Y_{m-1,n}，Y_{m+1,n}，Y_{m,n-1}，Y_{m,n+1}\}$。需要注意的是，在边界点处的像素，其邻域个体少于4个。

综合上述两种情况，我们有如下的马尔科夫随机场的图结构：

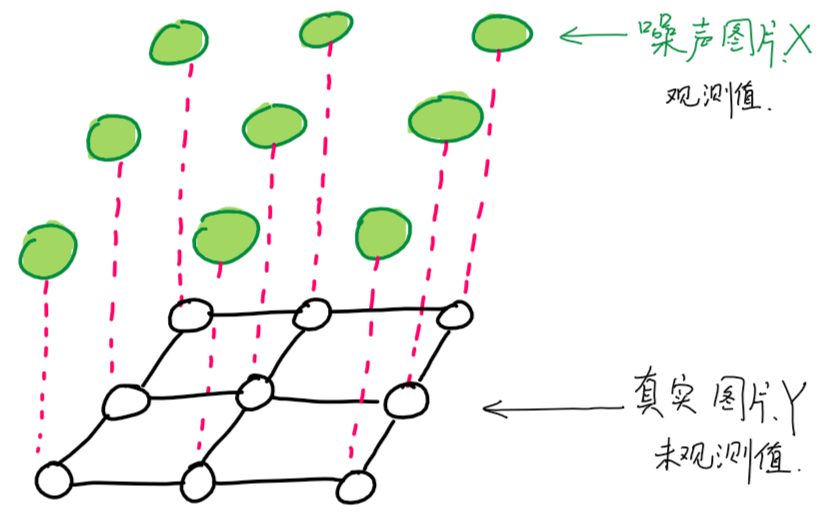
值得注意的是，我们看到这种结构的马尔科夫随机场，其最大团即是任意一条边连接的两个顶点.

为了后续公式看起来更简洁，我们用单下标来索引矩阵中的像素点，即$i=(m,n)$，这样$X_i$即表示矩阵中第$i$行$j$列中的像素点。需要注意的是：此时$i=1,2,\cdots,M\times N$，即$i$的最大下标是$MN$.

目前为止，我们还没有讨论势函数$\phi$的具体形式。实际上，除了要求$\phi$严格为正外，我们可以根据实际情况设置满足自己要求的函数形式，通过这种方式，我们加入了自己的领域知识(Domain Knowledge),这给我们研究问题带来了很大的灵活性。在此问题中，针对(a)和(b)两种情况，我们将$\phi$定义为指数函数的形式，即：

(a) $\phi_a (X_i,Y_i)=\exp{\left(\alpha X_i Y_i\right)}$
(b) $\phi_b (Y_i,Y_i)=\exp{\left(\beta Y_i Y_j\right)},\quad X_j\in Nb(X_i)$

上式中，$\alpha$和$\beta$是参数。先对(a)进行分析，有下表：
\begin{array}{rrr}
\hline
X_i & Y_i & X_iY_i \\
\hline
1 & 1 & 1 \\
1 & -1 & -1 \\
-1& 1 & -1 \\
-1 & -1 &1\\
\hline
\end{array}

我们令随机变量的取值为$\pm 1$，分别代表黑色和白色两种情况。我们注意到，当$X_i$与$Y_i$相同时，他们的积为1；当$X_i$与$Y_i$不相同时，他们的积为-1，这正好符合直觉—噪声图像上的像素点总是与真实图像对应位置上的像素点取值相同。$X_iY_i$值越大，就代表两个像素点是相同的。

同理，对(b)进行分析，我们也得到相似的结论，同样符合直觉：真实图像的像素点总是与其邻域内的像素点的取值相同。我们同样希望$Y_iY_i$越大越好。

有了(a)(b)两种情况下的势函数，我们就可以直接写出联合概率密度函数。该马尔科夫随机场中，每一个边所连接的两个顶点就是一个最大团，因此团的数目和边的数目是相等的。

$\begin{aligned} P(X,Y)&=\frac{1}{Z}\prod_i \left(\phi_a (X_i,Y_i)\prod_{j\in Nb(i)}\phi_b (Y_iY_j)\right)\\ &= \frac{1}{Z}\prod_i\exp{\left(\alpha X_iY_i +\sum_{j\in Nb(i)} \beta Y_iY_j\right)} \\ &= \frac{1}{Z} \exp{\left[\sum_i \left(\alpha X_iY_i +\sum_{j\in Nb(i)} \beta Y_iY_j\right)\right]} \end{aligned}\tag{3}$

我们希望对(3)最大化，即最优的

$\begin{aligned} \mathbf{y}^{*}&= \mathop{\arg\,\min}_{Y} \quad P(X,Y)\\ \color{red}{log函数单调性\rightarrow}&=\arg\max_{Y} \quad \log{P(X,Y)}\\ \color{red}{带入式(3)\rightarrow}& =\mathop{\arg\,\min}_{Y}\quad -\log{Z}+ \sum_i \left(\alpha X_iY_i +\sum_{j\in Nb(i)} \beta Y_iY_j\right)\\ \color{red}{Z是常数\rightarrow}&= \mathop{\arg\,\min}_{Y_i\in \{+1,-1\}\\ i=1,\cdots,M\times N}\quad \sum_i \left(\alpha X_iY_i +\sum_{j\in Nb(i)} \beta Y_iY_j\right) \end{aligned}\tag{4}$

我们注意到，上述公式实际上式关于变量$Y$的多变量的组合优化问题($X=\mathbf{x}$已经观测到，认为是常数)，很不幸的是，它是NP-hard问题，我们没办法得到其精确解。

然而，我们还是可以通多近似求解的方法求解，这里引入(Iterated Conditional Modes,ICM)方法，该方法的核心核心思想是，每次从优化只优化一个变量。具体来讲，对于变量集合$Y=\{Y_1,Y_2,\cdots,Y_{MN}\}$,我们选定一个下标$i$,令其他变量固定不变，即认为$Y_1,Y_2,\cdots,Y_{i-1},Y_{i+1},\cdots,Y_{MN}$固定不变，只对$Y_i$进行优化。这样，优化问题(4)就变为单变量优化问题：

$\begin{aligned} \mathbf{y}_i^{*}&= \mathop{\arg\,\min}_{Y}\quad \sum_i \left(\alpha X_iY_i +\sum_{j\in Nb(i)} \beta Y_iY_j\right)\\ \color{red}{其他变量认为是常数\rightarrow}&= \mathop{\arg\,\min}_{Y_i\in \{+1,-1\}}\quad \alpha X_iY_i +\sum_{j\in Nb(i)} \beta Y_iY_j\\ \color{red}{带入 Y_i=\pm 1\rightarrow}&= \mathop{\arg\,\min}\quad \pm\{ \alpha X_i+\beta\sum_{j\in Nb(i)}Y_j\}\\ \color{red}{简化形式\rightarrow}&= \text{sign} \{ \alpha X_i+\beta\sum_{j\in Nb(i)}Y_j\} \end{aligned}$

按照一定的顺序，$i$遍历所有的变量$Y_i,i=1,2,\cdots,M\times N$，我们就完成了一轮循环；重复该过程，直至一定最大循环次数。最终输出近似最优解$\mathbf{y}^*$。我们可以证明，引用该方法可能得到一个满意的局部最优解(不一定全局最优)。

至此，我们就完成了对图像去噪问题的建模过程和求解方法的讨论。接下来的工作是算法编程。

代码

我们应用Python实现算法编程（代码借鉴自文献2，并进行了部分修改）。

# -*- coding: utf-8 -*-
"""
Created on Sun Apr 22 00:12:18 2018
@author: handsomeboy
"""
import matplotlib.pyplot as plt # plt 用于显示图片
import matplotlib.image as mpimg # mpimg 用于读取图片
import numpy as np

import matplotlib.font_manager as font_manager
prop = font_manager.FontProperties(fname=r'C:\Windows\Fonts\msyh.ttf')

# preprocessing step 前处理阶段,将图像变为二元图
def read_image_and_binarize(image_file): 
  im = mpimg.imread(image_file)
  A = np.asarray(im).astype(int)
  A.flags.writeable = True

  A[A<0.5] = -1
  A[A>=0.5] = 1  
  return A 

#加入噪声
def add_noise(orig):
  A = np.copy(orig)
  
  for i in range(np.size(A, 0)):
    for j in range(np.size(A, 1)):
      r = np.random.rand()
      if r < 0.1:
        A[i][j] = -A[i][j]  #变为相反的
  return A

def denoise_image(X, alpha, beta):
  #核心，矩阵的长和宽  
  m, n = np.shape(X)
  
  # initialize Y same as X 初始化去噪后的图片
  Y = np.copy(X)
  
  # optimization 最大迭代次数
  max_iter = 10*m*n
  
  for iter in range(max_iter):
    # randomly pick a location 随机选一个位置
    i = np.random.randint(m)
    j = np.random.randint(n) #随机选一个位置
    
    # compute the log probabilities of both values of Y_ij 计算概率的log
    log_p = compute_log_prob(X, Y, i, j, alpha, beta)
    
    # assign Y_ij to the value with higher log probability 哪一个概率高就设置为哪一个
    Y[i][j]=np.sign(log_p)
    #输出迭代数目  
    if iter % 100000 == 0:
      print ('Completed', iter, 'iterations out of', max_iter)
  return Y

def compute_log_prob(X, Y, i, j, alpha, beta):
  result = alpha * X[i][j] 

  result += beta  * compute_log_prob_helper(Y, i-1, j)
  result += beta  * compute_log_prob_helper(Y, i+1, j)
  result += beta  * compute_log_prob_helper(Y, i, j-1)
  result += beta  * compute_log_prob_helper(Y, i, j+1)
  return result

def compute_log_prob_helper(Y, i, j):
  try:
    return Y[i][j]
  except IndexError:
    return 0

orig_image = read_image_and_binarize('ECUST.png')
orig_image=orig_image[:,:,1]

alpha = 8
beta  = 10
  
noisy_image = add_noise(orig_image)

# use ICM for denoising
denoised_image = denoise_image(noisy_image, alpha, beta)

plt.figure()

ax1=plt.subplot(311)
plt.imshow(orig_image,cmap='gray')
plt.title(u'原始图片',fontproperties=prop,fontsize=15)
ax1.yaxis.set_major_locator(plt.NullLocator()) 
ax1.xaxis.set_major_locator(plt.NullLocator()) 
  
ax2=plt.subplot(312)
plt.imshow(noisy_image,cmap='gray')
plt.title(u'噪声图片',fontproperties=prop,fontsize=15)
ax2.yaxis.set_major_locator(plt.NullLocator()) 
ax2.xaxis.set_major_locator(plt.NullLocator()) 

ax3=plt.subplot(313)
plt.imshow(denoised_image, cmap='gray')
plt.title(u'去噪图片',fontproperties=prop,fontsize=15)
ax3.yaxis.set_major_locator(plt.NullLocator()) 
ax3.xaxis.set_major_locator(plt.NullLocator()) 

plt.show() 
plt.savefig("Reaust.png",bbox_inches='tight')

上述程序中，mpimg.imread(image_file)读入的图像矩阵的值在[0,1]区间，我们以0.5为界，将低于0.5的像素点设为-1，高于0.5设为1。

实验结果

应用上述Python程序，我们得到以下结果：
去噪效果

可以看到，去噪后的图片与真实图片相当接近，去噪效果让人满意。定量地，我们在生成噪声图片时采用了10%的误差率，即整张图片有10%的像素发生的反转，我们计算真实图像与去噪图像的误差率，计算结果为0.6%，远小于10%，该数据跟我们的直觉相符。

讨论

在定义势函数时，我们引入了参数$\alpha$和$\beta$,具体取值人为设定。实际上，这两个参数对最终的去噪效果影响很大。下面给出了两组参数设置情况下的不同去噪效果的比较：

在具体应用中，设定最优的参数值，一般需要多次试验，通过多次尝试得到最合适的参数设定。当然，我们可以通过优化的方法来寻找最优的$\alpha$和$\beta$，但前提是需要一组(真实图像，噪声图像)的训练样本集合，根据这些样本，我们可以通过求最大似然函数的方法得到最优的 $\alpha^*$ 和 $\beta^*$ ,其中涉及的计算量比较大，感兴趣的同学请搜索相关文献。

总结

本博文针对噪声图像去噪问题展开研究，应用马尔科夫随机场对问题进行数学建模，将问题抽象为求最大后验概率密度函数的极值问题，并应用ICM方法将问题进一步分解为单变量优化问题并进行求解。实验证明，得到的去噪图片，去噪图片与真实图片的误差为0.6%，达到了满意的去噪效果。同时，本文还研究了参数$\alpha$和$\beta$变化时，对图像去噪效果的影响。

本文仅对二元黑白图像的去噪问题进行研究，灰度图像和彩色图像的去噪问题，请参见参考文献5。